Pohybující se elektrony (od kladného pólu zdroje k zápornému), narážejí ve vodiči na kmitající ionty krystalové mřížky a svůj pohyb zpomalují. Říkáme, že vodič klade elektrickému proudu odpor.

Elektrický odpor je vlastnost látky omezit průchod usměrněných elektronů vodičem.
1. Budeme-li k stejnému zdroji elektrického napětí postupně zapojovat vodiče z různých látek, ale o stejné délce a stejném průřezu, ampérmetrem změříme, že každým vodičem protéká elektrický proud jiné velikosti. Každý materiál totiž klade průchodu proudu jiný odpor.
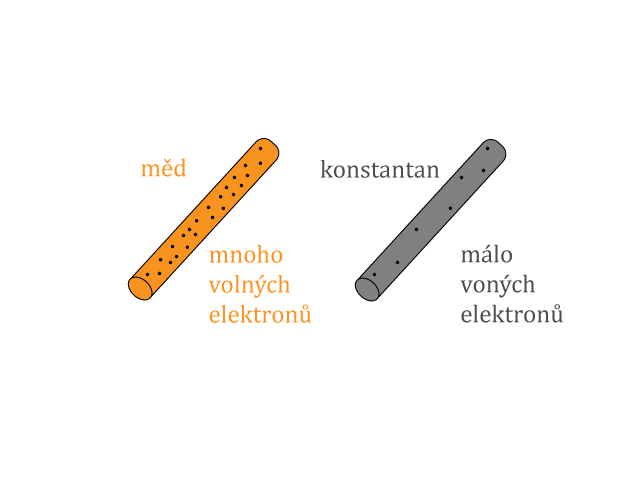
2. Použijeme-li k měření vodiče vyrobené z jedné látky, které budou mít stejný průměr, ale vždy různou délku, ampérmetrem zjistíme pro každou délku vodiče jiný procházející proud. Největší proud proteče nejkratším vodičem.
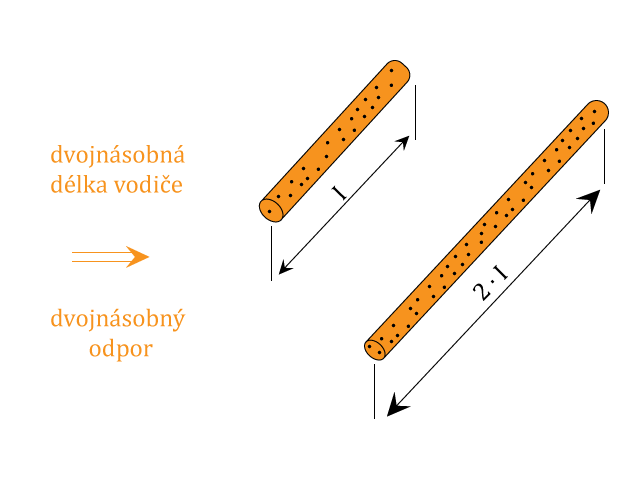
3. Použijeme-li k měření vodiče vyrobené z jedné látky o stejné délce, ale různých průřezech, změříme různé hodnoty proudu pro každý vodič s jiným průřezem. Největší proud proteče vodičem s největším průřezem.
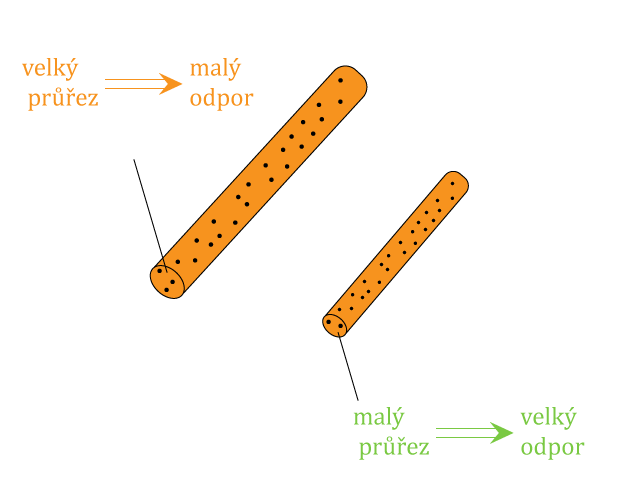
Elektrický odpor vodiče závisí na materiálu, z kterého je vodič vyrobený, jeho délce a průřezu vodiče.
$$ R = ρ \cdot \frac{l}{S} $$
Závislost elektrického odporu na materiálu vodiče vyjadřuje veličina měrný elektrický odpor (rezistivita).
Měrný elektrický odpor je odpor vodiče o délce 1m a průřezu $ 1mm^2 $. Čím menší hodnotu má měrný elektrický odpor, tím lépe látka vede elektrický proud.
Materiál | Složení | ρ |
Cín | Sn | 0,115 |
Hliník | Al | 0,028 |
Kantal A-1 | 72 % Fe, 20 % Cr, 5 % Al, 3 % Co | 1,45 |
Konstantan | 54 % Cu, 45 % Ni, 1 % Mn | 0,49 |
Měď | Cu | 0,018 |
Mosaz | 50 - 99 % Cu, Zn | 0,075 |
Platina | Pt | 0,11 |
Stříbro | Ag | 0,017 |
Tantal | Ta | 0,155 |
Uhlík (grafit) | C | 0,33 - 1,85 |
Zlato | Au | 0,0235 |
Železo | Fe | 0,098 |
Zdroj:
Mikulčák a kolektiv: Matematické, fyzikální a chemické tabulky pro střední školy, SPN Praha, 1988
Měděné vodiče mají malý elektrický odpor. Měděný drát o průměru 2mm a délce 100m má odpor jen 0,54Ω. Železný drát stejných rozměrů má odpor 3,12Ω a drát z kanthalu (slitina Fe,Cr,Al,Co) dokonce 44,6Ω.
Odpor vodičů se mění s teplotou.
Při běžných teplotách $ 0^{\circ} C – 100^{\circ} C $ tato změna probíhá lineárně.
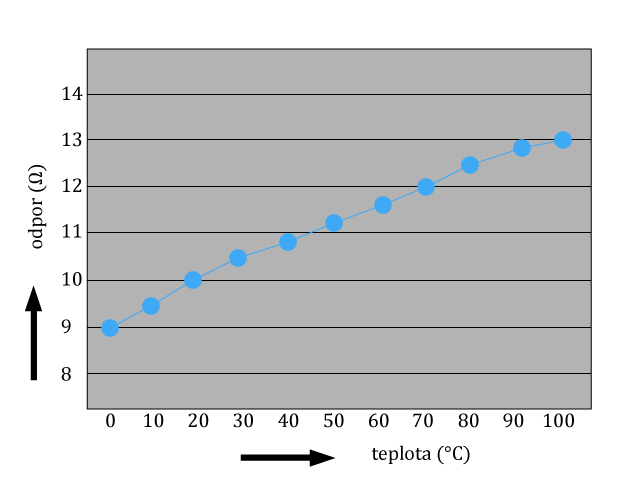
Výsledný odpor při teplotě t vypočítáme ze vzorce
$$ R = R_0 ( 1 + αΔt ) $$
Veličina α je teplotní součinitel odporu $ K^{-1} $.
Teplotní součinitel odporu určuje změnu odporu 1 Ω, při změně teploty o $ 1^{\circ} C $.
Pro měď $ α = 0,0039 K^{-1} $ a pro hliník $ α = 0,0037 K^{-1} $.
Ohřejeme-li měděný vodič o odporu 1 Ω o teplotu $ 10^{\circ} C $ změní se jeho odpor o 0,039 Ω a bude mít hodnotu 1,039 Ω.
U většiny čistých kovů je při běžných teplotách jeho hodnota blízká hodnotě $ 4 \cdot 10^{-3} K^{-1} $.
U kovů s rostoucí teplotou jejich odpor vzrůstá, u nekovových vodičů klesá.
U některých slitin (například u konstantanu) se odpor s teplotou téměř nemění. Využívá se toho u reostatů.
Lineární změny elektrického odporu s teplotou se využívá v odporových teploměrech. V plynových troubách a kamnech jsou tyčové termostaty
Kromě teploty má na změnu odporu u některých látek vliv také magnetické pole a světlo. Například u vizmutu, železa a niklu se odpor mění v magnetickém poli a selen snižuje svůj odpor při osvětlení až na setinu původní hodnoty.
Při velmi nízkých teplotách, které jsou blízké absolutní nule (-273,15 K) je kmitavý pohyb molekul tak nepatrný, že se v nich volné elektrony pohybují bez jakéhokoliv odporu. Proud zavedený do takto silně ochlazeného vodiče teče stále a bez sebemenších ztrát. Pozorujeme tzv. supravodivost.
Kamerling Onnes postupným ochlazováním platinových a zlatých vzorků zjistil, že jejich elektrický odpor klesá tak, jak to předpověděl již Dewar. Když svůj experiment dělal se rtutí, při teplotě asi 4,27 K začal její odpor prudce klesat a při teplotě asi 4,22 K úplně vymizel. V následujících letech objevil supravodivost i u dalších kovů.
Jaká je jeho hmotnost?
Jak velký bude odpor tohoto vodiče při teplotě $ 40^{\circ} C $?