Střídavý proud, střídavé napětí a jejich vzájemný vztah jsou ovlivněné nejen frekvencí, ale také vlastnostmi obvodu. Střídavý obvod mohou tvořit různé prvky, které jsou charakterizované svými parametry. Parametrem rezistoru je jeho odpor R, parametrem cívky je indukčnost L a parametrem kondenzátoru je kapacita C. Obvody, které se skládají pouze z jednoho spotřebiče, se nazývají jednoduché obvody střídavého proudu. Obvody, které se skládají z více různých spotřebičů, se nazývají složené obvody střídavého proudu.
Parametry obvodu střídavého proudu mají vliv nejen na velikost proudu a napětí, ale také ovlivňují jeho fázi
Fáze
Značka: $ φ $
Jednotka: rad
Fáze určuje hodnotu napětí a proudu v obvodu v čase $ t = 0 \, s $. Důležitější než fáze samotná je tzv. fázový rozdíl mezi počáteční fází napětí a proudu v obvodu.
Předpokládejme, že obvod je tvořen rezistorem a zdrojem střídavého napětí. Připojíme-li do obvodu žárovku, zjistíme, že rezistor v obvodu má stejný účinek na žárovku, jako kdyby byl připojen ke zdroji stejnosměrného napětí (zvyšuje odpor v obvodu).

Odpor se chová v obvodu střídavého proudu stejně jako v obvodu stejnosměrného proudu. Zmenšuje velikost elektrického proudu v obvodu.
Odpor R, který klade vodič střídavému proudu, se nazývá rezistance.
Rezistance
Značka: R
Jednotka: Ω
Výpočet: $ R = \frac{U_m} {I_m} $
Pokud budeme sledovat časový průběh napětí a proudu, zjistíme, že napětí a proud dosahují ve stejný okamžik maximální hodnotu a ve stejný okamžik nulové hodnoty.
Mezi napětím a proudem je nulový fázový rozdíl $ φ = 0 $rad.

Proud a napětí jsou v obvodu střídavého proudu ve fázi.
Pro velikost napětí a proudu na čase platí:
$$ u = U_m \cdot sin \cdot \omega \cdot t $$
$$ i = I_m \cdot sin \cdot \omega \cdot t $$
Ohmův zákon pro část obvodu platí v obvodu s rezistorem jak pro maximální hodnoty napětí a proudu, tak pro hodnoty okamžité.
$$ I_m = \frac{U_m}{R} $$
$$ i = \frac{u}{R} = \frac{U_m \cdot sin ( \omega \cdot t )}{R} $$
Z grafu určete rezistanci, periodu, frekvenci, úhlovou frekvenci a zapište rovnice okamžité hodnoty napětí a proudu na čase.

Předpokládejme, že obvod je tvořen cívkou a zdrojem střídavého napětí. V tomto obvodu kromě ohmického odporu R existuje ještě odpor, který klade průchodu proudu cívka. Tento odpor nazýváme induktance. Budeme předpokládat, že máme k dispozici ideální cívku. V ideální cívce můžeme ohmický odpor zanedbat a předpokládáme, že jediným odporem je induktance.
Induktance
Značka: $ X_L $
Jednotka: Ω
$$ X_L = \frac {U_m} {I_m} $$
Charakteristickou vlastností cívky je indukčnost, proto můžeme induktanci vyjádřit:
$$ X_L = \omega \cdot L $$
Čím větší je indukčnost cívky, tím větší odpor klade cívka průchodu elektrického proudu. Tento odpor vzniká v důsledku vlastní indukce. Vlivem nestacionárního magnetického pole v obvodu se v cívce indukuje napětí namířené svými účinky proti napětí zdroje. Protože velikost indukovaného napětí závisí na rychlosti změn magnetického pole, můžeme říci, že velikost induktance se zvětšuje s rostoucí frekvencí střídavého proudu.

Odpor v obvodu střídavého proudu s cívkou (induktance) je tím větší, čím větší je indukčnost cívky a čím větší je frekvence střídavého proudu. Indukčnost cívky je větší u cívek s uzavřeným jádrem a roste s rostoucím počtem závitů.
$$ X_L = 2 \pi fL $$
Indukčnost cívky má vliv nejen na velikost induktance, ale také na fázový posun mezi napětím a proudem v obvodu. Víme, že vlivem vlastní indukce v cívce chvíli trvá, než začne procházet elektrický proud.
V obvodu střídavého proudu s cívkou napětí předbíhá proud.
Proud se za napětím zpožďuje o čtvrtinu periody, fázový rozdíl je
$$ φ = - \frac{\pi}{2} rad $$

Pro velikost napětí a proudu na čase platí:
$ u = U_m \cdot sin \ \omega \cdot t $
$ i = I_m \cdot sin \ (\omega \cdot t - \frac {\pi} {2}) $
Z grafu určete induktanci, indukčnost cívky, periodu, úhlovou frekvenci a zapište rovnice okamžité hodnoty napětí a proudu na čase.

Vypočítejte velikost proudu, který bude procházet cívkou o indukčnosti $ 1,4 \, H $, jestliže ji zapojíme do zásuvky elektrické sítě.
Předpokládejme, že obvod je tvořen kondenzátorem a zdrojem střídavého napětí. Kondenzátor je součástka, která v sobě „shromažďuje“ náboj. Jestliže ho zapojíme do obvodu se zdrojem stejnosměrného napětí, kondenzátor se nabije a přeruší průchod proudu v obvodu. Žárovka v obvodu svítit nebude.
Jestliže použijeme zdroj střídavého napětí, bude se kondenzátor díky změnám směru proudu pravidelně nabíjet a vybíjet a jestliže bude kapacita kondenzátoru dostatečně velká, žárovka bude svítit.

Odpor, který vytváří v obvodu kondenzátor, se nazývá kapacitance. Kapacitance je tím menší, čím větší je kapacita kondenzátoru.
Kapacitance
Značka: XC
Jednotka: Ω
$$ X_C = \frac {U_m} {I_m} $$
Charakteristickou vlastností kondenzátoru je kapacita. Kapacitanci můžeme také vyjádřit:
$$ X_C = \frac {1} {\omega \cdot c} $$
Stejně jako velikost induktance, tak i velikost kapacitance závisí na rychlosti změn magnetického pole.
Odpor v obvodu střídavého proudu s kondenzátorem (kapacitance) je tím větší, čím menší je kapacita kondenzátoru a čím menší je frekvence střídavého proudu.
$$ X_C = \frac{1}{2 \pi fC} $$
Kapacita kondenzátoru má vliv také na fázový posun mezi napětím a proudem v obvodu. Jestliže je kondenzátor vybitý, napětí mezi jeho deskami je nulové a nabíjecí proud je největší. U nabitého kondenzátoru je napětí mezi deskami největší a proud neprochází. Z toho lze vyvodit, že napětí mezi deskami kondenzátoru se zvětšuje postupně.
V obvodu střídavého proudu s kondenzátorem se napětí zpožďuje za proudem.
Proud předbíhá napětí o čtvrtinu periody, fázový rozdíl je $ φ= \frac{\pi}{2} rad. $
.
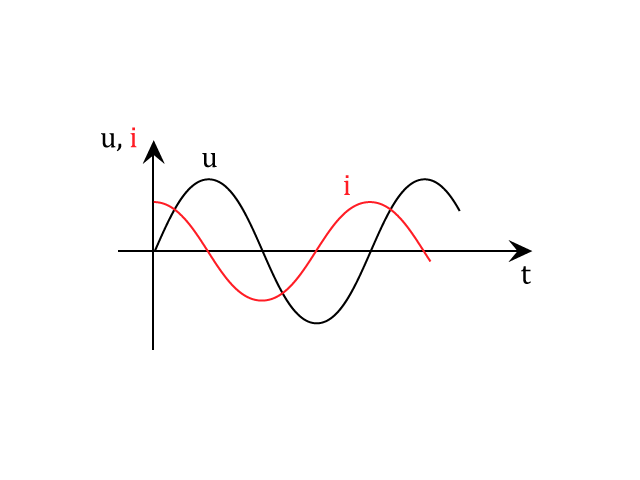
Pro závislost velikosti napětí a proudu na čase platí:
$$ u = U_m \cdot sin \cdot \omega \cdot t $$
$$ i = I_m \cdot sin (\omega \cdot t + \frac {\pi} {2} ) $$
Z grafu určete kapacitanci, kapacitu kondenzátoru, periodu, úhlovou frekvenci a zapište rovnice okamžité hodnoty napětí a proudu na čase.

Všechny tři prvky jsou v obvodu zapojené podle obrázku.


Z vyšrafovaného trojúhelníku můžeme matematicky vyjádřit velikost napětí U a odvodit vzorec pro odpor v sériovém RLC obvodu. Tento odpor nazýváme impedance.
Po dosazení:
$ U^2 = U_p^2 + (U_L - Uc)^2 $
$ (I \cdot Z)^2 = (I \cdot R)^2 + (I \cdot X_L - I \cdot X_C)^2 $
$ I^2 \cdot Z^2 = I^2 \cdot R^2 + I^2(X_L - X_C)^2 $
$ Z^2 = R^2 + (X_L - X_C)^2 $
$ Z = \sqrt{R^2 + (X_L - X_C)^2} $
Impedance
Značka: Z
Jednotka: Ω
Impedance je celkový odpor obvodu střídavého proudu.
$$ Z = \frac {U_m} {I_m} $$
$$ Z = \sqrt{R^2 + (\omega \cdot L - \frac {1} {\omega \cdot C})^2} $$
Ze stejného trojúhelníku můžeme určit i fázový posun.
$$ tg φ= \frac{\omega \cdot L - \frac {1} {\omega \cdot C}} {R} $$
Zvláštním případem sériového RLC obvodu je takový, kdy induktance a kapacitance mají stejnou hodnotu a $ Z = R $. Takový obvod má při zapojení všech součástek vlastnosti rezistance.
Z grafu určete impedanci, periodu, frekvenci, fázový posun a zapište rovnice proudu a napětí na čase.
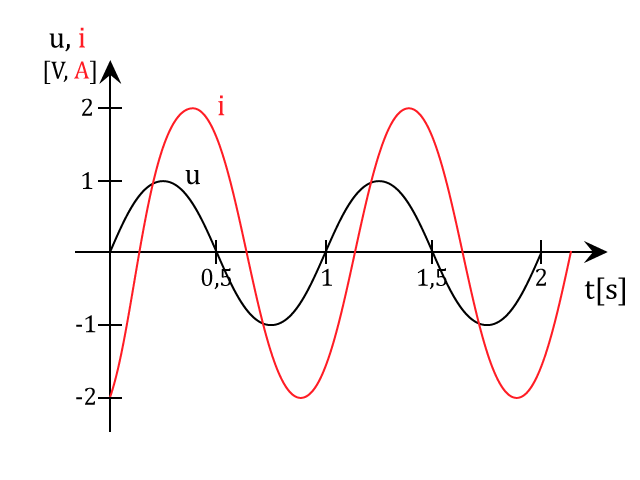
Kondenzátor o kapacitě 5 µF je připojen do obvodu střídavého proudu o frekvenci 50 Hz. Jakou indukčnost by musela mít cívka, aby měla v obvodu induktanci stejné hodnoty jako je kapacitance kondenzátoru.