V předchozích kapitolách jsme se dozvěděli, že na vodič s proudem v blízkosti magnetu působí magnetická síla. Také dva vodiče s proudem na sebe vzájemně působí magnetickou silou.
Působily by na sebe vzájemně magnetickou silou i vodiče, kterými elektrický proud neprochází?
Příčinou vzniku magnetického pole v okolí vodiče jsou pohybující se volné částice s nábojem. Magnetická síla působící na vodič je pak výslednicí magnetických sil působících na jednotlivé nabité částice. Dá se tedy předpokládat, že magnetická síla nebude působit jen na volné částice s nábojem ve vodiči, ale i na ty, které se pohybují samostatně mimo vodič.
Jestliže chceme zjistit, jaká magnetická síla působí na jeden elektron, můžeme použít vztah pro magnetickou sílu působící na vodič kolmý k magnetickým indukčním čarám.
$ F_m = B \cdot I \cdot l $
Protože elektrický proud je určen velikostí náboje, který projde průřezem vodiče za jednotku času a náboj je tvořen N elektrony, můžeme psát:
$ F_m = B \cdot \frac{N \cdot e}{t} \cdot l $
Vidíme, že velikost magnetické síly, která působí na náboj v magnetickém poli, závisí na velikosti náboje a jeho rychlosti.
$$ F_m = B \cdot Q \cdot v $$
Pohyb elektronů v magnetickém poli lze pozorovat ve Wehneltově trubici, která obsahuje zdroj elektronů zatavený v baňce naplněné vodíkem při nízkém tlaku. Trubice je umístěna v homogenním magnetickém poli. Ze zdroje vylétávají elektrony rychlostí $ \vec{v}$ a působí na ně magnetická síla, která zakřivuje jejich trajektorii. Vzhledem k tomu, že elektrony se pohybují po kružnicové trajektorii, je velikost magnetické síly rovna velikosti síly dostředivé.
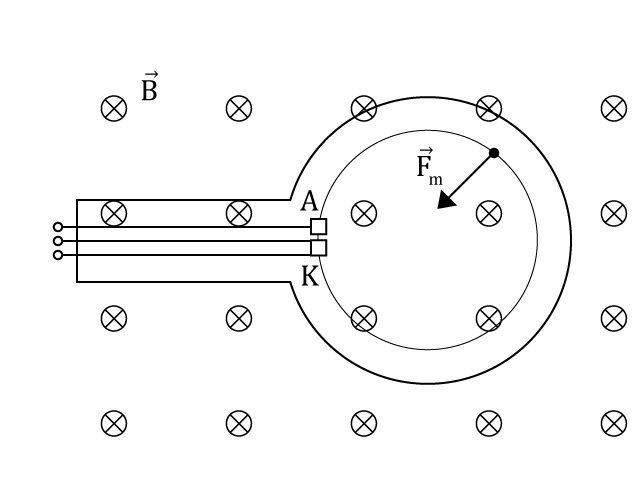
$$ F_m = F_d $$
Pro poloměr kružnicové trajektorie částice tedy platí:
$$ r = \frac{m \cdot v}{B \cdot Q} $$
$$ B \cdot Q \cdot v = \frac{m \cdot v^2}{r} $$
Pro rychlost pohybu částice platí:
$$v = \frac{B \cdot Q \cdot r}{m} $$
Vypočítejte poloměr kružnicové trajektorie, po které se pohybuje elektron rychlostí $ 10^5 m \cdot s^{-1} $. Magnetická indukce má velikost $ 25 \,mT $.
Magnetické pole působí na nabitou pohybující se částici magnetickou silou. Největší magnetická síla působí na částici, která se pohybuje kolmo k magnetickým indukčním čarám. Pohybuje-li se částice ve směru magnetických indukčních čar, magnetické pole na částici nepůsobí a žádná magnetická síla nevzniká.
Pohybuje-li se částice současně v magnetickém i elektrickém poli, působí na něj elektrická i magnetická síla. Jejich výslednicí je Lorentzova síla.
Pohybu nabité částice v magnetickém poli se využívá například k měření v mlžné komoře nebo při vychylování elektronového svazku v obrazovkách.
Vliv magnetického pole na urychlený elektron je využíván při konstrukci elektromagnetických čoček elektronových mikroskopů. Změna magnetického pole o indukci B se projeví změnou zakřivení trajektorie elektronu, tím se změní zaostřovací schopnost čočky a parametry zobrazení.
